数字图像处理

Github 的 README.md 并不支持公式的渲染，所以部分原理讲解的东西移到这个篇章的博客中。

本篇包含：

• 骨架提取
• 霍夫变换
• Canny 边缘检测
• Metric Rectification

Skeleton

前一段时间在看折痕消除的一篇论文的时候提到了提取文字的骨架，就重新复习一下《数字图像处理》这本书中关于骨架的知识。

集合 $A$ 的骨架的 $S(A)$ 概念上很简单：

若 $z$ 是 $S(A)$ 的一点，$D_z$ 是 $A$ 内以 $z$ 为圆心的最大圆盘，则不存在包含 $D_z$ 且位于 $A$ 内的更大圆盘，满足这些条件的圆盘 $D_z$ 称为最大圆盘

若 $D_z$ 是一个最大圆盘，则它在两个或多个不同的位置与 $A$ 的边界接触。

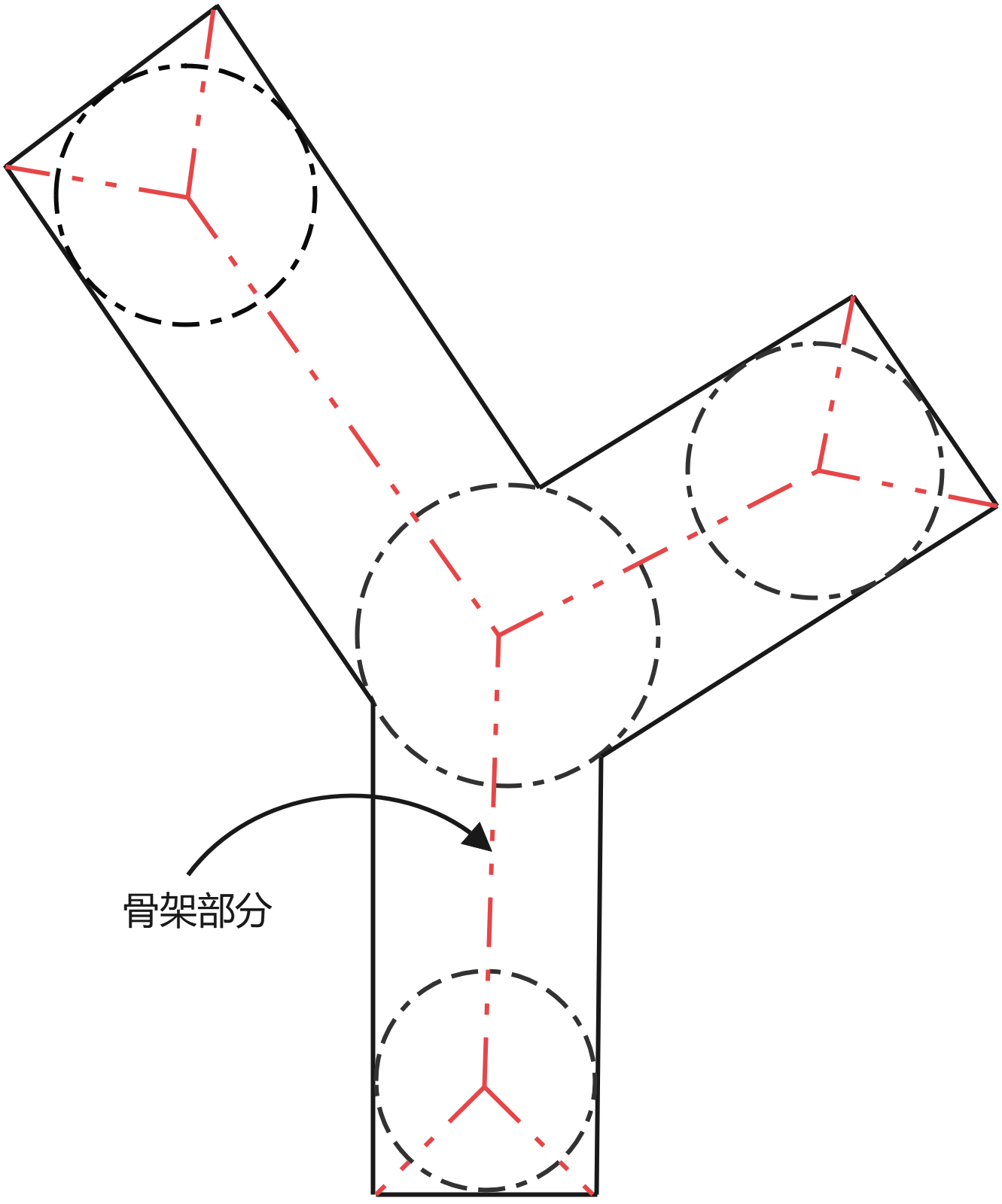
$A$ 的骨架可以用腐蚀和开运算来表示：

$$S(A) = \bigcup_{k=0}^{K}S_k(A)= \bigcup_{k=0}^{K}(A\ominus kB)-(A\ominus kB)\circ B$$

式中，$B$ 是一个结构元，$A\ominus kB$ 表示 $A$ 的连续 $k$ 次腐蚀，同时，$K$ 是 $A$ 被腐蚀为一个空集前的最后一个迭代步骤：

$$K = max\{ k| A\ominus kB \ne \oslash \}$$

Canny

只使用梯度做边缘检测的一个很大的问题是：对噪声过于敏感，所以提出了 Canny 边缘检测算子。

Canny 算法基于以下三个目标：

• 低错误率：所有边缘都应该被找到，并且不应有虚假响应。
• 边缘点应该被很好的定位：已定位的边缘必须尽可能接近真实边缘，也就是说，由检测子标记为边缘的一点和真实边缘的中心之间的距离应最小。
• 单个边缘点响应：对于每个真实的边缘点，监测子应该只返回一个点，也就是说，真实边缘周围的局部最大数应该是最小的，这意味着检测子不应识别只存在单个边缘的多个边缘像素。

与之对应的，Canny 边缘检测包含 5 个步骤：

• 平滑（Suppress noise）
• 梯度计算（Compute gradient magnitude and direction）
• 非最大值抑制（Apply non-maximum suppression）
• 滞后阈值法/双阈值法（Hysteresis thresholding/Double thresholding）
• 连通性分析（Connectivity analysis to detect edges）

首先采用高斯模糊来平滑图像。令 $f(x, y)$ 表示输入图像，并令 $G(x, y)$ 表示高斯函数：

$$G(x, y) = e^{-\frac{x^2+y^2}{2 \sigma^2}}$$

用 G 和 f 的卷积得到平滑后的图像 $f_s(x, y)$

在这之后计算梯度幅度和方向：

$$M_s(x, y) = || \nabla f_s(x, y) || = \sqrt{g_x^2(x,y)+g_y^2(x, y)} \\ \alpha(x, y)=\mathrm {arctan} \left [ \frac{g_y(x,y)}{g_x(x,y)} \right ]$$

由于梯度图像通常在局部极大值附近包含一些宽脊，下一步非极大值抑制就是细化这些宽脊。

我们首先将所有可能的边缘方向量化为 4 个方向范围，如 0,45,90,135 如果该点处梯度的幅值小于该方向上的相邻两个点（在该点两侧），则抑制（赋值为 0），否则不变。

得到的图像 $g_N(x,y)$ 是只包含细化边缘的结果，然后我们对 $g_N(x,y)$ 进行阈值处理，以减少假边缘点。 Canny 算法使用滞后阈值处理，一个高阈值 $T_H$ 和一个低阈值 $T_L$。高低阈值的比率应该在 2 到 3 之间。

阈值运算可以看做创建了两个新的图像 $g_{NH}$ 和 $g_{NL}$

$$g_{NH}(x,y)=g_N(x,y) \ge T_H \\ g_{NL}(x,y)= T_H \gt g_N(x,y) \ge T_L$$

这两个分别代表“强”边缘像素和“弱”边缘像素，所有的强边界像素均被假设为有效的边缘像素，并被立即标记，如果弱边缘的像素连接到了强边缘（8邻域），则这些弱边缘也被认为是图像的边界，所以最后一步就是用BFS 判断一遍弱边缘是不是连接到了强边缘，如果连接到了，该点也可以认为是强边缘，就从该点继续向 8 邻域搜索。

Hough Transform

已知一副图像中的 n 个点，假设我们希望找到这些点中位于直线上的子集，一种可能的解决方法是。首先找到由每对点确定的直线，然后寻找特定直线的哪些点的所有子集。这种方法涉及寻找 $\frac{n(n-1)}{2}\sim n^2$ 条直线，然后将每个直线执行 $n*\frac{n(n-1)}{2}\sim n^3$ 次比较，计算困难。

Hough 提出了一种方法，通常称为霍夫变换。令 $(x_i, y_i)$ 表示 $xy$ 平面上的一点。并考虑一条直线的斜截式：

$$y_i=a x_i +b$$

满足过点 $(x_i, y_i)$ 的直线有无数条，此时我们考虑 $ab$ 平面，并将直线改写成为：

$$b=-x_i a +y_i$$

在该空间下，通过原直线的两个点 $(x_i, y_i), (x_j, y_j)$ 一定在某个点相交，这个点就是直线的斜率和截距。事实上，直线上的所有的点在该平面上都相交于一个点。

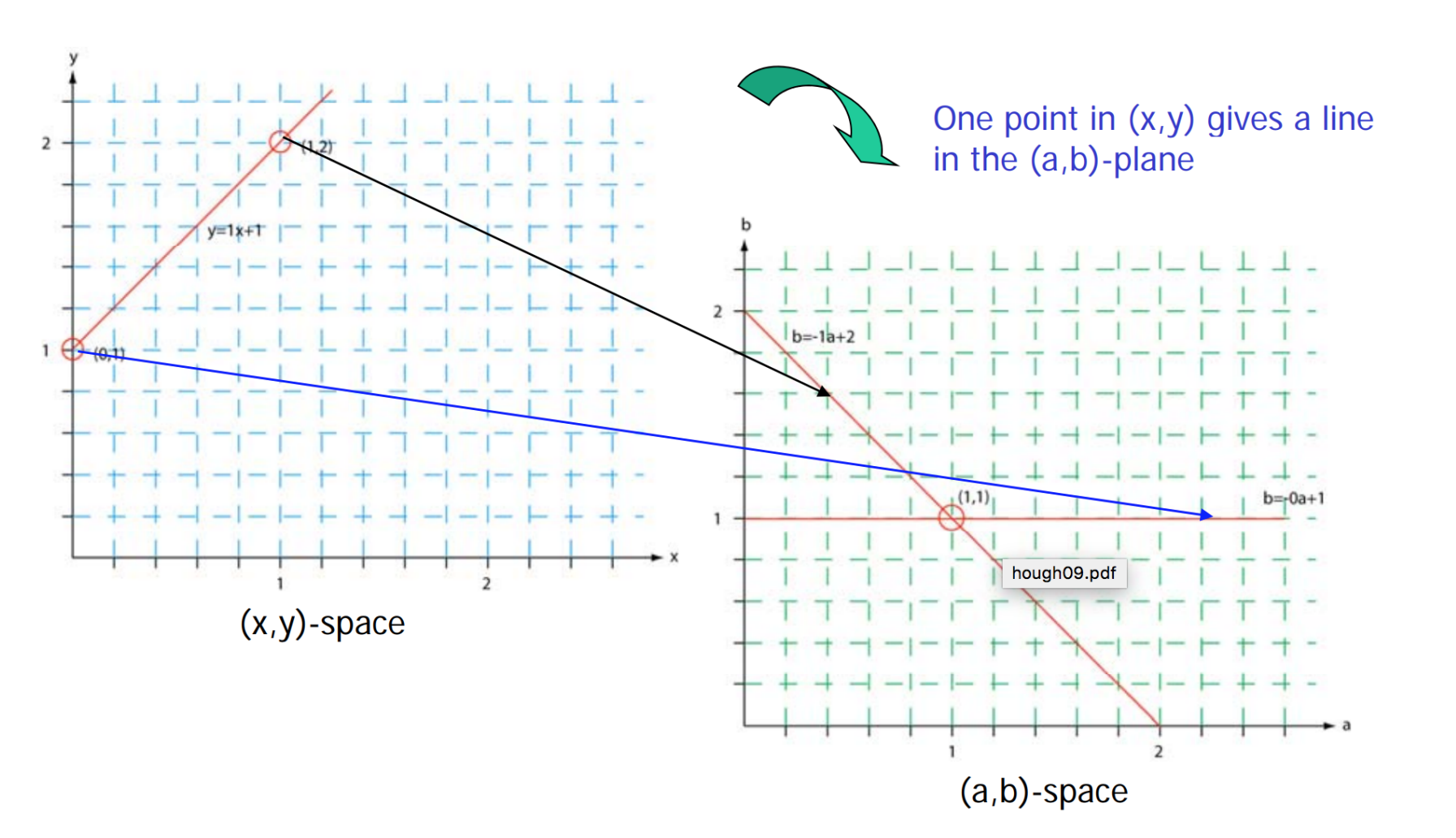
为了解决直线斜率无穷大的问题，我们用另外一种直线的标准式：

$$x \cos \theta+y \sin \theta=\rho$$

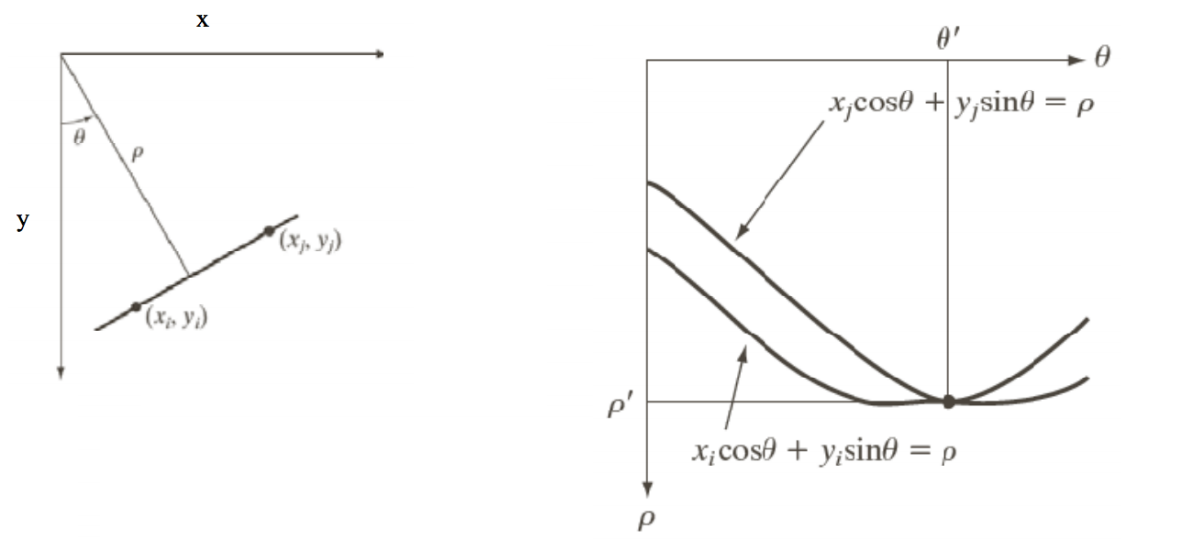
在具体的算法计算上，霍夫变换首先将参数空间划分为多个累加单元。假设其中$(\rho_{min}, \rho_{max})$ 和 $(\theta_{min}, \theta_{max})$ 是期望的参数值范围。坐标 $(i, j)$ 处具有累加值 $A(i,j)$ 的单元对应参数空间 $(\rho_i, \theta_j)$ 的方格。最初，这些单元格被设置为 0，对 $xy$ 平面的非背景点 $(x_k, y_k)$，对于所有可以取的 $\theta$，求得 $\rho$，将该值四舍五入到 $\rho$ 轴上最接近的单元格，若选择一个 $\theta_q$ 的值解得 $\rho_p$，则令：

$$A(p, q) = A(p, q) + 1$$

最后，当 $A(i, j)$ 大于一个特定的值时，认为存在一条对应的直线。

Metric Rectification

我们需要首先知道 3D 视觉中常见的几种变换

• 相似性（similarity）变换：由各向同性缩放组成的等距映射

$$\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right)=\left[\begin{array}{ccc} s \cos \theta & -s \sin \theta & t_{x} \\ s \sin \theta & s \cos \theta & t_{y} \\ 0 & 0 & 1 \end{array}\right]\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)$$

也可以写作矩阵块的形式如：

$$x^{\prime}=H_{S} x=\left[\begin{array}{ll} s R & t \\ 0^{T} & 1 \end{array}\right] x$$

• 仿射变换（affine）变换：保持二维图形的“平直性”，即变换后直线还是直线不会打弯，圆弧还是圆弧和“平行性”，平行线还是平行线，相交直线的交角不变。

$$x^{\prime}=H_{A} x=\left[\begin{array}{cc} A & t \\ 0^{T} & 1 \end{array}\right] x$$

其中 $A$ 是 2×2 的非奇异矩阵。平面仿射变换有6个自由度，对应6个矩阵元素。而它总可以分解为：

$$A=R(\theta) R(-\phi) D R(\phi)$$

其中 $R(\theta)$ 和 $R(\phi)$ 是两个旋转角度，D 是对角矩阵

$$D=\left[\begin{array}{cc} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right]$$

该分解可以通过 SVD 分解实现。

• 单应性 （homography） 变换：也叫投影变换

$$x' = H_p x = \begin{bmatrix} A & t\\ V^T & v \end{bmatrix} x$$

其中 $v=(v_1,v_2)^T$。

投影和仿射变换之间的主要区别在于，对于投影变换，向量 $v$ 不为 null，这是投影变换非线性的原因。

比较理想点 $(x_1,x_2,0)^T$ 在仿射和投影变换下的不同：

仿射变换：

$$\left[\begin{array}{cc} A & t \\ 0^{T} & 1 \end{array}\right]\left(\begin{array}{c} x_{1} \\ x_{2} \\ 0 \end{array}\right)=\left(\begin{array}{c} A\left(\begin{array}{c} x_{1} \\ x_{2} \end{array}\right) \\ 0 \end{array}\right)$$

投影变换

$$\left[\begin{array}{cc} A & t \\ V^{T} & v \end{array}\right]\left(\begin{array}{c} x_{1} \\ x_{2} \\ 0 \end{array}\right)=\left(\begin{array}{c} A\left(\begin{array}{c} x_{1} \\ x_{2} \end{array}\right) \\ v_{1} x_{1}+v_{2} x_{2} \end{array}\right)$$

在仿射变化中，理想点保持理想状态（即无穷大）。 在投影变换中，它映射到一个有限点。

要完成图像的度量矫正，我们需要两点：消除投影变换和仿射变换带来的变化

遵循下面的步骤：

1. 寻找在图像平面中的平行的点来确定无穷远处的直线表达式。
2. 由于该线在原本的 3D 坐标系中的无穷远位置移动到了一个有限的位置，我们首先就需要将其回归到无穷远处，即寻找一个变换 $H_p$ 将 $l = (l_1, l_2, l_3)^T$ 变换到 $(0, 0, 1)^T$

我们一般选择

$$H_p = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -l_1/l_3 & -l_2/l_3 & 1/l_3 \end{bmatrix}$$

1. 对于图像的每一点应用该变换即可

这时图像中平行的线就会平行了，下一步需要矫正角度让垂直的线也能垂直。

1. 首先先选择好在原始场景中互相垂直的线的端点，在图像中选择这些点构成了新的线和新的夹角。

我们需要计算 $C^{*}_{\infty}$。对于每一组垂直的线，我们有约束，这些约束构成了一个可以解的方程组：

$$(l_1 m_1, (l_1 m_2 + l_2 m_1) / 2, l_2 m_2, (l_1 m_3 + l_3 m_1) / 2, (l_2 m_3 + l_3 m_2) / 2, l_3 m_3) C = 0$$

1. 根据奇异值分解计算可得变换矩阵，对于上一步变换完的结果再乘上该矩阵即可。

详细过程参考 Learn-DIP 中的代码。