最近复现论文的时候，遇到了一个实现细节的问题：双线性插值技术（bilinear interpolation）

简单来说，插值指利用已知的点来“猜”未知的点的属性值，图像领域插值常用在修改图像尺寸的过程，当然我遇到的这个问题不是简单的调个函数就能解决了的，我需要在一个凸四边形中用四个顶点来表示中心点，在中心点的坐标已知的情况下。

双线性插值

双线性插值运用在图像上，就是用原图像的四个点计算新图像的一个点，这个我们已经很熟悉了：

很容易能够推导：

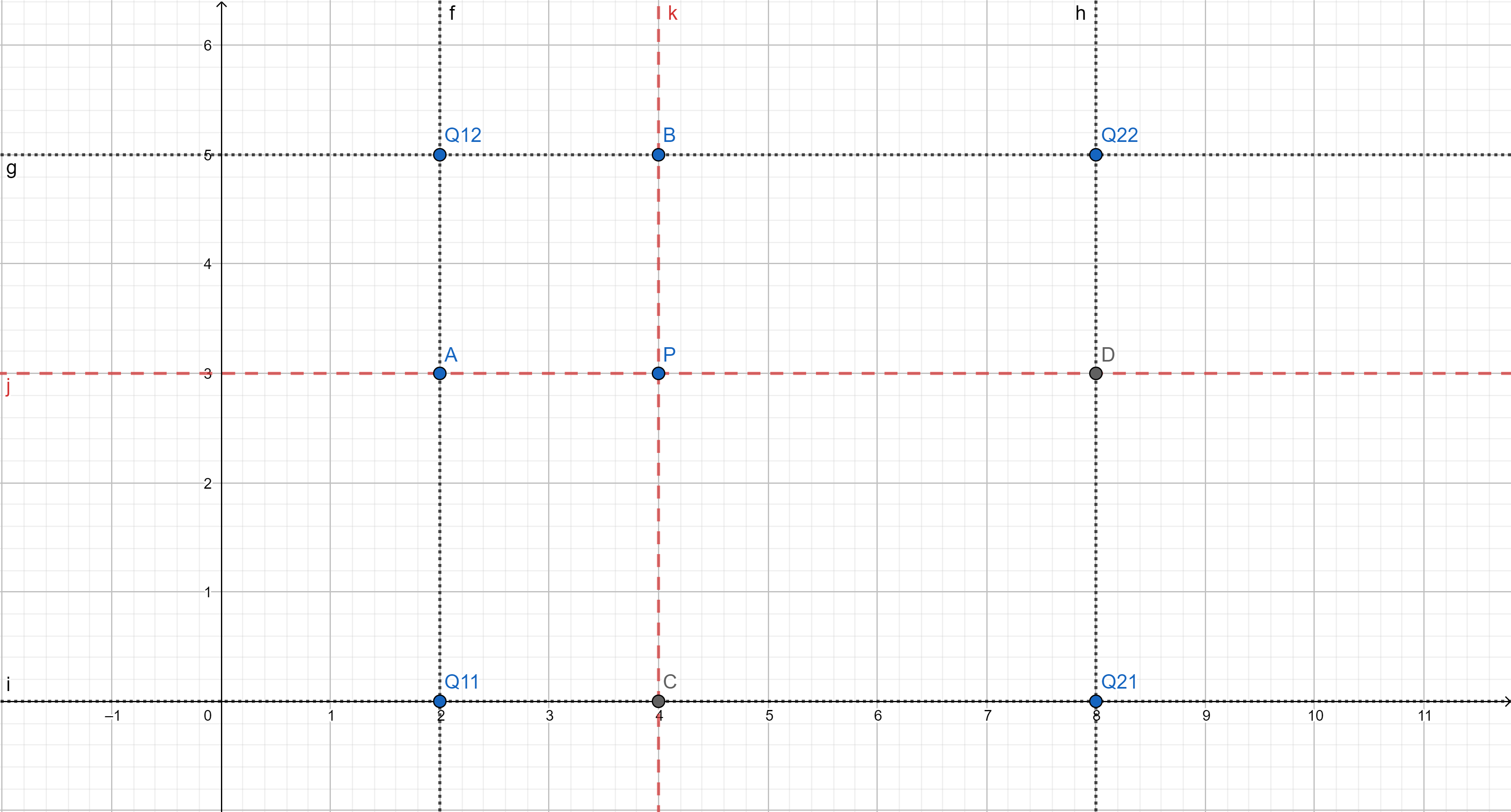
如果已知 要求 的坐标，我们很容易可以通过等比例的公式得出

对于 P 在 y 方向上做线性插值，有：

将第一步的结果代入第二步，得到结果：

对于图片的双线性插值，四个点的选择必然是相邻的，即
简化的形式如下：

数学推广

继续深入，双线性插值本质是个数学的问题，它可以被应用在图像大小变化等一些场合中。

In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables (e.g. x and y) on a rectilinear 2D grid

我遇到的就是这样的一个问题是，我的四个点并非是矩形，而且我希望可以用一种方法来让这四个点近似表示 P 点。
简单来说：

对于非对齐的输入点的双线性插值（Bilinear interpolation with non-aligned input points）

我们的外部不再是一个矩形了，我们定义 ，这时我们应该怎样用双线性插值的方法表示 P?

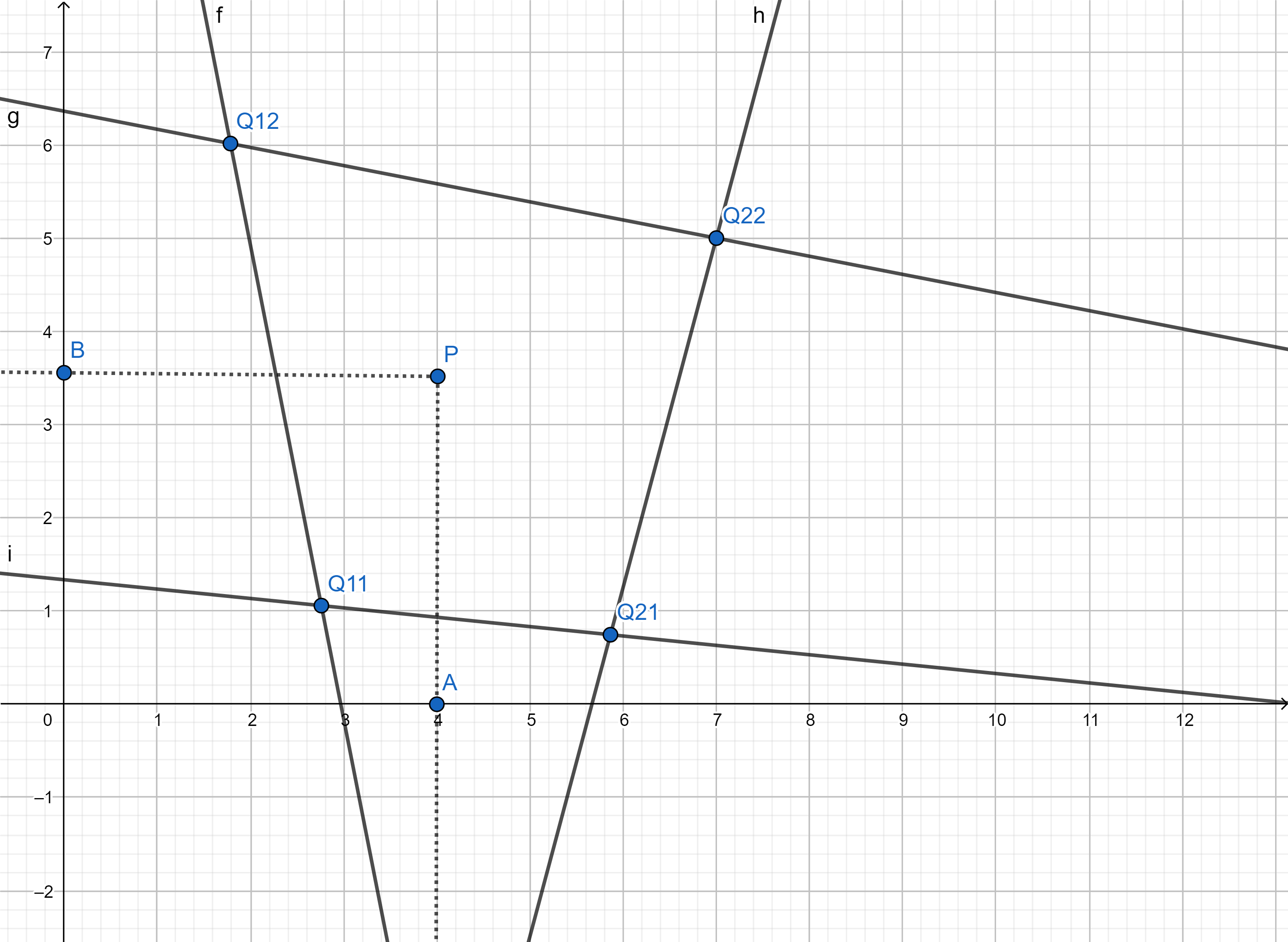
为了方便求解，我们转化一下，我们用这种方法来近似表示 P 点，t 和 s 是插值的系数，他们都是处于 0 和 1 之间的数，代表一个相对的权重系数。这样， P 可以用 s 和 t 来表示：

化简一下就得到了最终的表达式：

怎么解这样的一个方程，当然可以用牛顿法等一些近似数值解的算法，但解析解也是可以找到了！

我们首先先展开上面的式子，它对于 x 和 y 有相似的表示：

根据这两个等式，可以解出来 t

上面两个式子应该相等，这样我们就能联立得到一个伯恩斯坦形式的二次方程（Bernstein polynomial），他有更加优美并且数值上稳定的解，当然用一般二次方程的解也是没有问题的：

A, B, C 代表常数系数，最终的解为：

我们需要的 s 应该在 0 和 1 之间，往往得到的两个解会舍弃其中的一个。

• 当 时，对应线性的情况，此时 而 的情况理论上不会发生。

当时矩形的时候

最后一步就是带回 s 求解 t，选择前面的两个式子中的任意一个均可以。

这样就确定了解，就像论坛里说的一样 You can bilinearly interpolate in any convex tetragon. 它其实并不像想象中的那么复杂，就是简单的求解一个交点的问题。

逆双线性插值

我还见到一种方法叫做逆双线性插值(inverse bilinear interpolation)，引用文章里面的图来说明计算过程：

(其实和前面的基本思路是一样的，只是名字或者看上去不太一样)

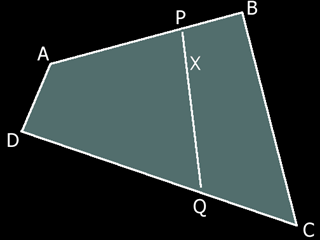
• 我们将 P 看做是 A, B 的按照系数 u 线性插值的位置点
• 我们将 Q 看做是同样系数的线性插值的位置点
• X 是 P 和 Q 的线性插值

这样 X 就可以用 u 和 v 来表示：

X 已知，我们需要多个方程才能解出来 u 和 v，而恰好，上面的式子，在 2 维空间下就有 x 和 y 两个式子，所以肯定有解。

定义下面几个临时变量：

简化后的等式：

对于任意两个象限 i,j（i, j 可以是 {x, y}, {y, z} …），以 x, y为例
解得

带回，有：

是不是觉得这个式子很熟悉，就是前面的，不过他转换成了一般二次方程的形式，一些小细节的地方也不太一样。主要是它可以完美的扩展到高维情况（虽然我暂时想不到高维的时候有啥用）

文章最后给出的伪代码：

float cross( in vec2 a, in vec2 b ) { return a.x*b.y - a.y*b.x; }
vec2 invBilinear( in vec2 p, in vec2 a, in vec2 b, in vec2 c, in vec2 d )
{
    vec2 res = vec2(-1.0);
    vec2 e = b-a;
    vec2 f = d-a;
    vec2 g = a-b+c-d;
    vec2 h = p-a;
    float k2 = cross2d( g, f );
    float k1 = cross2d( e, f ) + cross2d( h, g );
    float k0 = cross2d( h, e );
    // if edges are parallel, this is a linear equation
    if( abs(k2)<0.001 )
    {
        res = vec2( (h.x*k1+f.x*k0)/(e.x*k1-g.x*k0), -k0/k1 );
    }
    // otherwise, it's a quadratic
    else
    {
        float w = k1*k1 - 4.0*k0*k2;
        if( w<0.0 ) return vec2(-1.0);
        w = sqrt( w );
        float ik2 = 0.5/k2;
        float v = (-k1 - w)*ik2;
        float u = (h.x - f.x*v)/(e.x + g.x*v);
        
        if( u<0.0 || u>1.0 || v<0.0 || v>1.0 )
        {
           v = (-k1 + w)*ik2;
           u = (h.x - f.x*v)/(e.x + g.x*v);
        }
        res = vec2( u, v );
    }
    return res;
}

代码

我在想要怎样才能让这个方法独立于不同的数据结构（Eigen 或者 OpenCV 的 Vec，原生的 Point 类型），写一个好的模板函数出来。

参考链接

• Bilinear interpolation with non-aligned input points （里面有大佬的牛顿法迭代求解）
• 双线性插值 Bilinear Interpolation
• inverse bilinear interpolation
• Inverse Bilinear Interpolation?
• Bernstein Polynomial