数字图像处理

• 2021/5/28: 增加了部分示例代码

小波变换

小波 (Wavelet) 是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。有人把小波变换称为“数学显微镜”。

而对于图像处理相关领域，小波变换曾经相当的热门，一些经典的算法如 JPEG-2000 就是基于小波变换原理的。

要理解小波变换，有一大堆需要铺垫的东西…

多分辨率金字塔（Image Resolution Pyramids）

一般情况下，我们要处理的都是一张具有固定分辨率的图片，但有些时候，我们会对同一图像的不同分辨率的子图像进行处理，这些子图像往往是根据原图下采样得到的，如果我们将最大的图像放在底部，最小的放在顶部，就能得到一个金字塔的形状。图片金字塔可以用于图像融合，不过这不是我们在这里需要关注的。

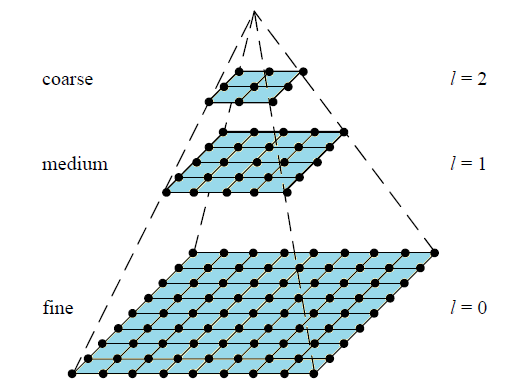
下采样的方法有很多，比如高斯金字塔：顶部图像中每个像素等于下一层图像中5个像素的高斯加权平均值。这样我们将一个 的图像变成了 大小的图像。

我们可以通过一个大图，通过高斯金字塔生成的方法得到多个小分辨率的图，但是，当我们通过金字塔顶层的图片来试图复原原图的时候，我们复原后的图会很“糊”，因为我们在下采样的时候丢失了图片的一些细节。

有没有一种变换可以不丢失细节，我们通过金字塔的顶层和一些其他的东西也可以复原出来原图像？

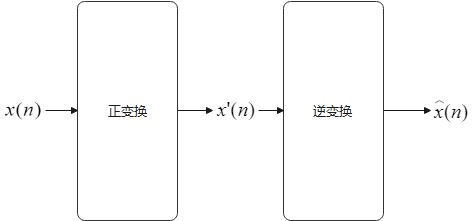
我们先在一维研究一下这个问题，如下图：

我们想要通过一组变换将 变换 然后再通过一个反变换得到 ，使得 ：

子带编码（Subband Coding）

子带编码一种以信号频谱为依据的编码方法，将信号分解成不同频带分量来去除信号相关性（可以理解成正交分解），再将分量分别进行取样、量化、编码，从而得到一组互不相关的码字合并在一起后进行传输。

如果我们可以把 按照高频和低频分解，在根据一种方法重组，根据子带编码的理论，我们可以无失真的重建 。

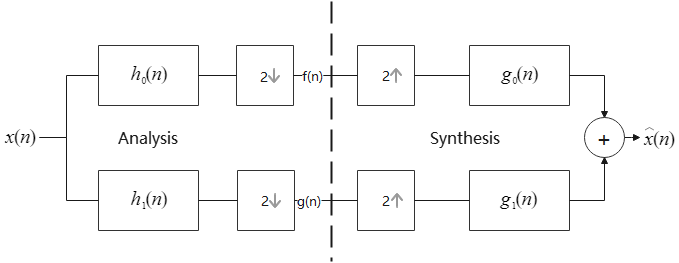
现在，我们只需要找到一组 就可以无失真重建了，我们可以将这一组的函数看做是一组一维的滤波器。

上/下采样（Upsampling/Downsampling）

我们首先对 做 Z 变换：

在时间域我们做因数为 2 的下采样可以等价到在 Z 域（复频域）的计算：

对应上采样的计算：

---

我们已经知道了如何上下采样了，现在只需要找到变换的函数了。根据数学公式的一堆推导（详细的参考课本，这里不再写了），我们可以得到关系式：

满足上面的关系的 H 和 G 函数都可以。

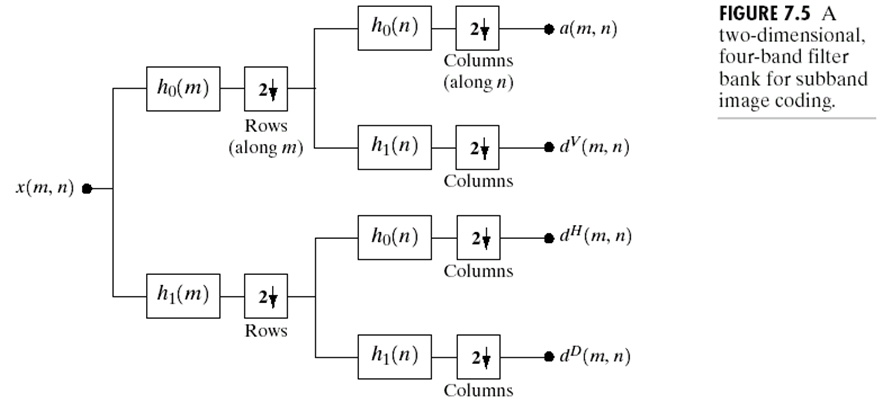
对于一个图像，我们只需要在行和列上分别应用子带编码就可以得到图像的滤波器了：

哈尔变换（The Haar Transform）

哈尔变换基于哈尔函数 ，就是满足上面的一组函数，他们定义在0到1之间。

为了便于理解，我们先将哈尔变换近似为另一种基于矩阵的变换。函数变成了我们表示为矩阵相乘：，其中 F 是 的图像, A 是 的变换矩阵，T 是变换的结果。而对于逆变换，有 。

下面给出生成哈尔变换矩阵 A 的方法：

对于任意的一个整数 u，它可以被唯一分解为

p 是 u 中包含的最大的 2 幂次，而 q 是余数，定义哈尔基函数：

哈尔矩阵的第 i 行包含了

如一个 4 阶的哈尔变换矩阵

这样我们就构造好了变换：先按照上面的方法用对应的 计算 T，然后下采样，再用对应 计算 T…，要恢复的时候就用逆变换的公式得到 F，再上采样，再逆变换…

基函数&尺度函数

我们理解了如何用矩阵去实现上面的子带编码的计算和恢复，但很明显，用矩阵的计算复杂度高，消耗时间，并且对于非正方形的图像需要补齐才能运算，带来了一定的误差。

尺度函数用于创建函数或图像的一些列逼近，每个逼近的分辨率与其最邻近逼近的分辨率相差 2 倍。并且使用称为小波的补函数对相邻逼近之间的差进行编码。简单来说就是通过尺度函数+小波函数来对频率域的图像进行近似。

这里开始就进入小波变换的内容了，**离散小波变换（DWT）**使用小波和一个尺度函数，将函数或者图像表示为小波和尺度函数的线性组合。

我们考虑由实的，平方可积的父尺度函数 的所有整数平移和二元缩放组成的基函数集合 ，其中：

整数 k 决定了平移的结果，尺度 j 决定了缩放（宽度和幅度），若固定 j，我们可以得到一个基函数的空间 ，增大 j 可以扩大这个空间，让更多的变换后的基函数加入到其中，也就能表示更多更小的细节。

哈尔尺度函数

我们还以哈尔为例，考虑高度为 1，宽度为 1 的尺度函数。

由这个父函数生成的一系列尺度函数：

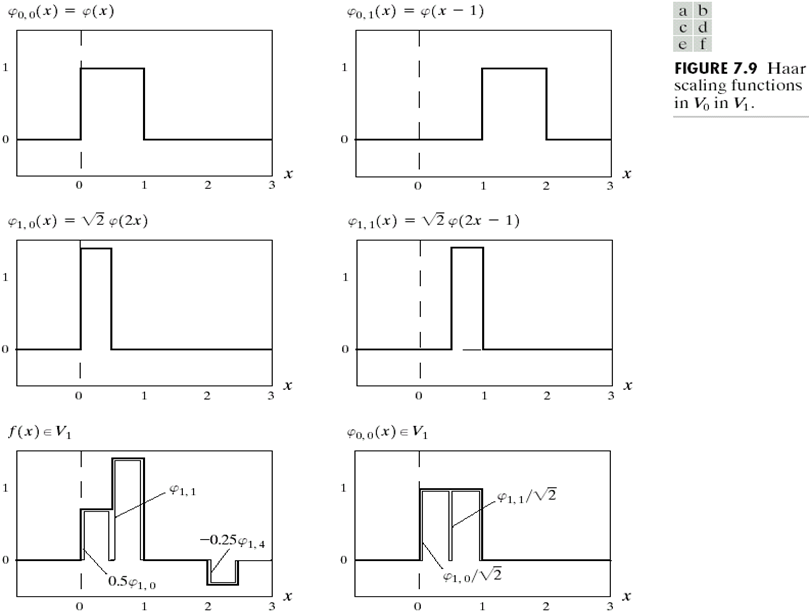
而一个略微复杂的函数 （e 图），可以用这些同一个尺度空间的尺度函数线性表示。

上面是在尺度空间 中的表示，我们同样也可以用 尺度空间来表示，只需要将上面的尺度空间 的基函数变换到 空间即可：

回忆起 的定义，根据上面我们发现的规律， 可以表示为自身 2 倍分辨率副本的线性组合。（取 j=1）

上式被称为膨胀方程，我们将展开的系数 称为尺度函数系数。

对于哈尔尺度函数，可以计算出他的尺度函数的系数 ：

小波函数

我们现在理论化前面的规律，对小波函数进行一般性的描述：

对于所有的 ，存在一个母函数$\psi_{j,k}(x)=2^{\frac{j}{2}} \psi(2^jx-k) $，若令 表示由小波函数 张成的函数空间，则：

表示函数空间集合的并集，并且作为 的基的尺度函数和作为 的基的小波函数是正交的：

尺度函数和小波空间的关系如下图：

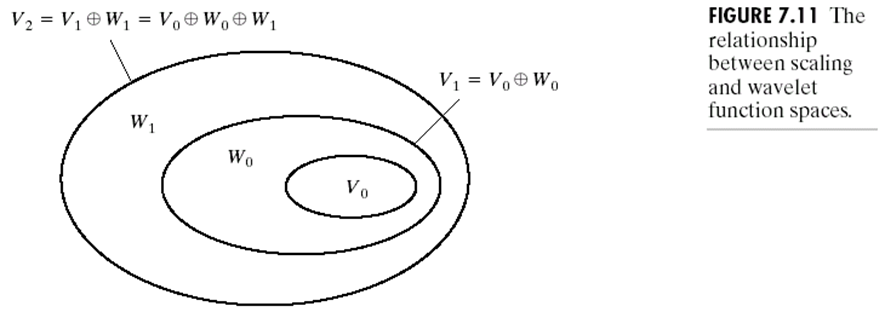
小波函数（类似于前面提到的尺度函数）可以用平移且分辨率加倍后的尺度函数的加权和来表示，我们可以写出：

其中 被称为小波系数。

可以证明：

对于一个不在函数空间内的一个函数 ，可以把它写成小波函数和尺度函数的和

仍以哈尔小波函数为例，在前面我们计算出了哈尔尺度系数，可以求得对应的小波系数：

这两个系数对应 矩阵的第二行，代入小波函数的表达式可得 ，于是哈尔母小波函数是：

二维小波变换

一维小波变换很容易扩展到二维，在二维情况下，需要 1 个尺度函数和 3 个二维小波，每个二维小波都是两个一维的积。排除产生了 1 维结果的积之后，剩下的 4 个积产生可分离的尺度函数：

和可分离的“方向敏感”小波：

V, D, H 分别表示小波度量图像中灰度延行（垂直边缘），对角线，列（水平边缘）的变化，他们分别表示行，对角线，列的高频信息，而 就是图像的低频信息了。

课本上二维小波变换的示意图：

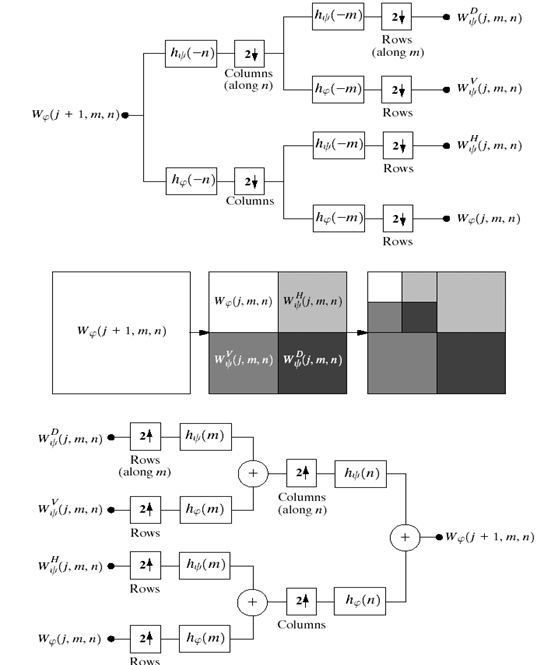
代码

Python 的 PyWavelets 包提供了小波变换的库。

官方文档给出的示例代码，对单张图片进行小波变换：

import numpy as np
import matplotlib.pyplot as plt

import pywt
import pywt.data


# Load image
original = pywt.data.camera()

# Wavelet transform of image, and plot approximation and details
titles = ['Approximation', ' Horizontal detail',
          'Vertical detail', 'Diagonal detail']
coeffs2 = pywt.dwt2(original, 'bior1.3')
LL, (LH, HL, HH) = coeffs2
fig = plt.figure(figsize=(12, 3))
for i, a in enumerate([LL, LH, HL, HH]):
    ax = fig.add_subplot(1, 4, i + 1)
    ax.imshow(a, interpolation="nearest", cmap=plt.cm.gray)
    ax.set_title(titles[i], fontsize=10)
    ax.set_xticks([])
    ax.set_yticks([])

fig.tight_layout()
plt.show()

LL, LH, HL, HH 分别代表低频信息，水平细节，垂直细节和对角线细节，结果如图：

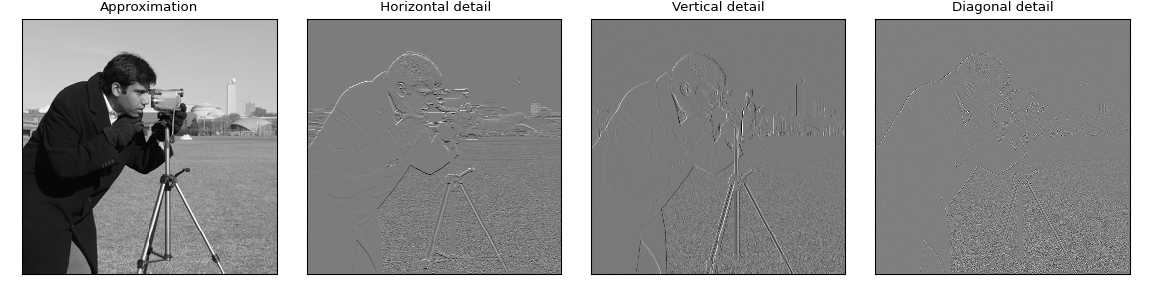
多阶小波

如果想要多阶的小波变换，就需要 wavedec2 函数，它的返回值是一个列表 [cAn, (cHn, cVn, cDn), … (cH1, cV1, cD1)] 第一个值是低频信息，第二个元组是从第 n 层到第 1 层 3 个维度的高频信息。

# ......
scales = pywt.wavedec2(img, "haar", level=4)
base = scales[0]
fourth_layer = scales[1]
third_layer = scales[2]
second_layer = scales[3]
first_layer = scales[4]
# ......

对于反变换，和傅里叶变换时使用的库的函数命名方式很相似，均是以 “ixxx” 开头的函数。如 dwt2 对应 idwt2， wavedec2 对应 waverec2，系数的形式要和使用 wavedec2 得到的结构一致。

小波去噪

后记

学起来的时候还真是反复看了好多边，再加上一些资料，才感觉有一丝丝的理解了…，真的难，本人菜鸡，有问题还请指出。

参考

• 数字图像处理第四版（冈萨雷斯）
• The Wavelet Tutorial
• 图像的多分辨率金字塔
• OpenCV教程（25）图像金字塔
• 小波变换和多分辨率处理（百度文库）
• 小波分析（百度百科）