aix

偏微分方程

• 学的时候记得笔记都是英语的加上又懒得翻译就只好拖到了现在

General

• 偏微分方程（PDE, partial differential equation）的解是一个关于时间和空间的方程 ，我们用 u 代表在特定时间和空间的函数值。

• 在常微分方程的数值解中，我们是通过将 0-T 划分为若干个 ，通过计算每个 位置的值来计算 。在偏微分方程中，我们构造下面的图形（mesh）来辅助我们的计算：

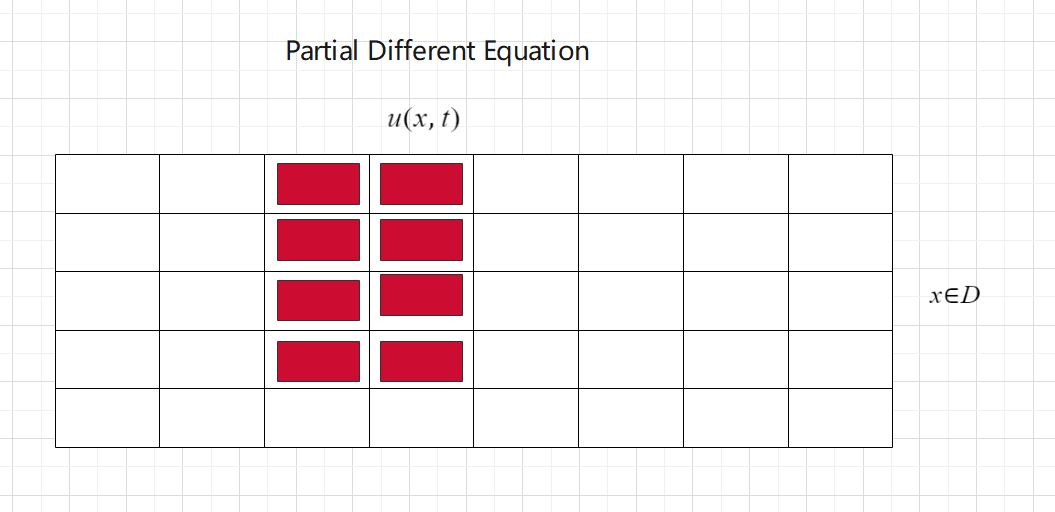
我们用 mesh 网格图上的 u 值来近似计算偏微分的值，我们观察临近的矩形，他们构成偏导的近似值。这样我们将偏微分方程的空间离散化，转换为常微分方程的系统。

空间离散化的方案(spatial discretization schemes)有：

• 有限元法（Finite Element Methods）
• 有限差分法（Finite Difference Methods）
• 有限体积法（Finite Volume Methods）

Finite Difference Formulas

我们以一个简单的偏微分方程为例：

k 代表导热系数。

假设网格在空间上的距离为 h，那么我们有:

• 一阶偏导的前向差分(Forward difference for first spatial derivative)

• 一阶偏导的向后差分(Backward difference for first spatial derivative)

• 一阶偏导的中心差分(Central difference for first spatial derivative)

• 二阶偏导的中心差分(Central difference for second spatial derivative)

Discretization Stencil

• 我们在网格来近似计算空间函数偏导（前向差分，中心差分等等）的这种方法叫做stencil，如果用空间内更多更远的点来近似一个点的偏导值，那么一般情况下误差就会变的更小。但对于有些情况却不同，补充的来说，用更多的点近似来减少误差只对光滑的函数有效，对于那些不连续的函数，相邻点之间的关系很小，使用太多的点反而会影响准确度。
• 我们用 stencils size 来描述有多少个点被用于近似偏导值。我们的误差和使用的近似方法的阶数成正比关系。我们假设误差为 e，h 为 网格缩小比例，q 是使用方法的阶数，我们有这样的关系：
• 需要注意：减小空间网格的大小的同时也要减小每一步的时间来确保稳定性。

Solving PDE

• 解决 PDE 问题就是解决一个初始边界值问题（initial boundary value problem）： 在给定的初始条件和边界条件下是如何变化的。

我们仍以热传导方程为例。在网格内部的点上，我们可以将求偏导转换为计算一组离散化的点，运用我们上面的二阶中心差分的近似计算：

我们想象 i 从 0 到 N-1，总共有 N-1 个类似上面的式子，即我们把 t 时间的 x 范围划分为 N-1 块，每一块都可以通过它临近的点来计算。下面把这 N-1 个式子合成在一起：

这样上面的方程就可以写成类似下面的形式：

f包含边界条件的信息。A 是一个 的系数矩阵，当x=1和x=N-1的时候都无法计算，所以设置行列式为全 0，需要 f 来辅助确定值以保证边界条件：

这样我们就可以用 ODE 的方法来解决 PDE 问题，比如说我们运用前向欧拉法：

We discretize the spatial domain into N spaces with N+1 grid points. How many unknown variables are evolved in the resulting system of ODEs?

答案是 N-1， 和 都是边界点（已知），这样在网格的内部就只有 N-1 个未知的点。

下面我们考虑计算的误差：PDE 方程的解的精确度分为空间和时间上的。我们取 e 代表误差，$\Delta t $ 代表每一步选择迭代的时间差(time_step)，h 代表相邻 x 之间的距离，也可以看做网格大小(mesh_size)，那么有关系：。其中 p 和 q 分别是我们选择的 ODE 方法的阶数和偏导数值解方法的阶数。如我们选择 FE (forward eluer) + 中心差分（Central Difference），那么 p 值为 1，q 值为 2。因为它们分别是 1 阶和 2 阶精确度的方法。如果 h 减小一半，那么误差就会变为四分之一。

需要注意，我们前面也提到了，一个小的 h 需要同时一个更小的 ，否则求解将会变得不再稳定。怎么理解呢，我们仍用热传导方程来理解：当我们观察更小的一段的变化的时候，不同段直接的交互会更加的频繁，我们需要用更小的时间来确保可以更加精确的捕获这些变化。

Boundary Conditions

• Dirichlet conditions

Dirichlet conditions fix the value of the solution u(x,t) at the boundary. This is like pinning the solution to a certain value at the boundary.

即在边界指定函数的分布形式

• Neumann conditions

Neumann conditions fix the value, not of the solution, but of its spatial derivative at the boundary. This is like fixing the stresses at the boundary.

在边界指定外法线方向上的导数的数值

• Robin conditions

Robin conditions fix the value of a linear combination of the solution itself and its partial derivative at the boundary.

可以看做是第1和2条件的组合，要求偏导和函数本身的数值。

Linear System

对于转换为 ODE 的 PDE 问题，我们也可以用一些隐式的方法求解，如隐式欧拉法

求解这个方法，移项：

它的每一步相当于求解一个线性系统（linear system）（这不就是线性方程组吗），
这么做的好处在于，这样让我们可以使用更大的 相比较于显式方法（隐式方法的稳定性，参考 ODE 那节）

求解线性系统有很多的现成方法：

• A 是一般矩阵（general）：高斯消元（Gaussian elimination），
• A 是三角矩阵（triangular）：Forward substitution/backward substitution，
• A 是三对角线矩阵（tri-diagonal）：托马斯算法（Thomas algorithm），

Iterative Algorithms for Linear Systems

当线性系统中的 M 是一个很大的矩阵，又不特殊时，用高斯消元太慢了并且太占用空间。这时就需要一个更高效的方法：迭代法再次上线。我们先猜一个初始值 v，通过计算 Mv 和 b 比较，修改 v 来一步步逼近真实解。

可选的迭代方法有很多，如 Krylov Subspace Method（krylov 子空间算法），conjugate gradients（共轭梯度法），GMRes（广义最小残差法）。

学一下共轭梯度法然后补充在这里

Nonlinear Systems

对于如下非线性形式的 ODEs：

使用隐式欧拉法得到迭代公式：

求解等同于在这样一个方程中寻找根:，常用的计算方法有：二分法，牛顿法

Sample

我们考虑污染物在一维空间的传播问题。令 表示在 t 时间 x 位置处污染物的浓度。u 的变化用对流扩散方程来定义：

扩散速率，对流速度$ c= 0.5m/s$
当 时污染物的分布图像为:

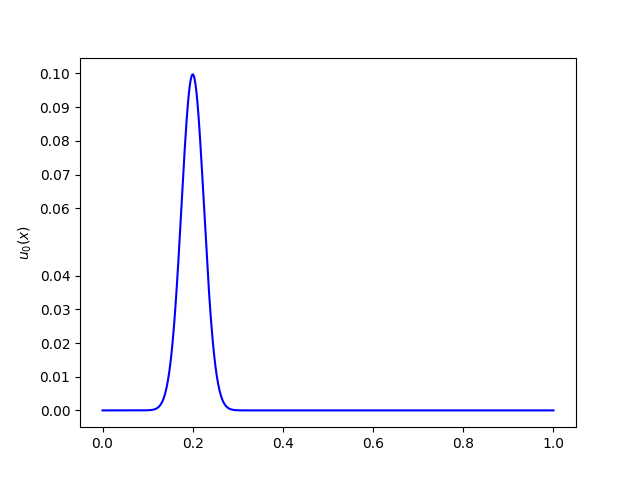
边界条件是第一类边界条件，在边界的时候始终等于 0。

我们采用有限差分法来计算污染物在 区间内随着时间从 0 变到 1 的变化。首先将偏导全部拆分近似为差分的形式：

然后用上面的方法转化为求 ODE 问题，代码如下：

import numpy as np
import math
import matplotlib.pyplot as plt


def u0(x):
    # 高斯函数
    mean = 0.2
    sigma = 0.025
    return (1/160)*np.exp(-1 * ((x - mean) ** 2) / (2 * (sigma ** 2))) / (math.sqrt(2 * np.pi) * sigma)


# init_ux():
# xs = np.linspace(0, 1, 1000)
# ys = [u0(x) for x in xs]
# plt.plot(xs, ys, "b-")
# plt.ylabel(r"$u_0(x)$")
# plt.yticks([round(x, 2) for x in np.linspace(0, 0.1, 10)])
# plt.savefig("init_ux.png")
# plt.show()
sample_num = 5
nSpace = 600
nTime = 1000
xs = np.linspace(0, 1, nSpace-1)
k = 5e-4
c = -0.5
dt = 1/nTime
h = 1/nSpace
A = np.zeros((nSpace-1, nSpace-1))
u = np.zeros((nSpace-1, 1))

for i in range(nSpace-1):
    u[i][0] = u0(i*h)

for i in range(1, nSpace-1-1):
    A[i][i-1] = k / (h * h) - c / h
    A[i][i] = (-2 * k) / (h * h) + c / h
    A[i][i+1] = k / (h * h)
# 采用欧拉方法
times = 0
t = 0
u_record = [u.T.tolist()[0]]
while t <= 1:
    u = u + dt * A.dot(u)
    t += dt
    times += 1
    # 每 200 次迭代记录一次
    if times == nTime/sample_num:
        u_record.append(u.T.tolist()[0])
        times = 0


# 采用二阶龙格库塔法
u = np.zeros((nSpace-1, 1))
for i in range(nSpace-1):
    u[i][0] = u0(i*h)
t = 0
times = 0

while t <= 1:
    k1 = A.dot(u)
    k2 = A.dot(u+k1*dt)
    u = u + 0.5 * dt * (k1 + k2)
    t += dt
    times += 1
    if times == nTime/sample_num:
        u_record.append(u.T.tolist()[0])
        times = 0

# 绘图
print(len(u_record))
values_fe = [int(i*250/10) for i in range(10)]
values_rk2 = [int(i*250/10) for i in range(10)]
colors_fe = ["#%02x%02x%02x" % (120, int(g), 200)for g in values_fe]
colors_rk2 = ["#%02x%02x%02x" % (200, int(g), 40)for g in values_rk2]

for i in range(sample_num):
    if i == 0:
        plt.plot(xs, u_record[i], color="#000080", linewidth=2, label="Init u")
    elif i == 1:
        plt.plot(xs, u_record[i], color=colors_fe[i], linewidth=2, label="FE Method")
    else:
        plt.plot(xs, u_record[i], color=colors_fe[i], linewidth=2)
for i in range(sample_num):
    if i == 0:
        plt.plot(xs, u_record[sample_num + i], color=colors_rk2[i], linewidth=2, label="RK2 Method")
    else:
        plt.plot(xs, u_record[sample_num + i], color=colors_rk2[i], linewidth=2)

plt.title("Evolution of u")
plt.xlabel("x")
plt.ylabel("u(x, t)")
plt.legend(loc="best")
plt.savefig("ux.png")
plt.show()

向后差分 + 显式欧拉 和 向后差分 + 二阶龙格库塔 方法得到的预测结果，颜色深度的变化代表时间的变化，绘制的图形为每隔 200ms 后在 x 上污染物的分布情况。：

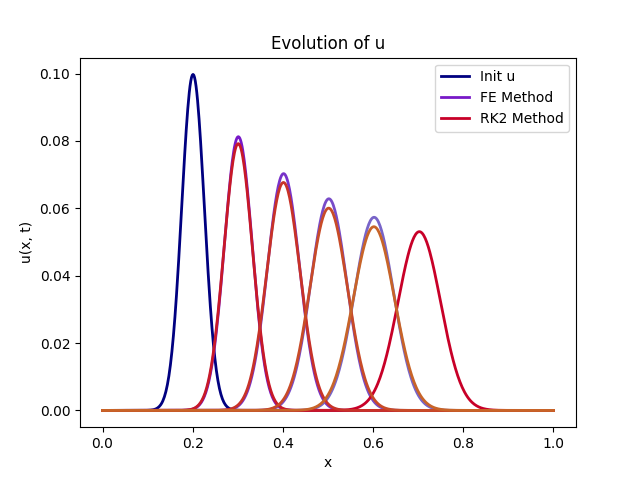
FE 误差为 8% 左右，如果我们使用 RK2 代替 FE 方法，误差减小到 0.8%。（用的黑盒函数测的误差，暂时还没复现解析解）

可以尝试修改 nSpace 和 nTime 观察效果。当切换方法为向前差分时，很难让结果稳定，对 nSpace 和 nTime 的要求很苛刻。