aix

正式开课了，这里仅是我的学习记录。

Module 1

introduction

Now, engineering and science applications may, as you know, have very different demands. Accuracy and reliability may be paramount(=very important). Large data sets might or might not be available. And we might need to use prior physical knowledge with new data-driven insights. We need to really combine physical modeling with what data can tell us.

The computational paradigm change over centuries:

• The experiment based model such as Newton’s Laws of Motion, we just observe carefully and distill the pricinple from thousands of experiments.
• The theory based model. It describe the physical world with a great deal of predictive power, accuary, and generalizability.
• The computational modeling and simulation. Based on the ideas that we use the computer to help us broaden the theory based model.
• The data-driven model. Using the machine learning method which gives us powerful ways of rebuilding models together with making predictions.

Module 2：常微分方程

they are equations that describe how things vary in time.

they are equation that describe how certain things vary in space.

they can be understood as a very deep limit of a recurrent neural network.

…

常微分方程的一般形式是

其中 u 代表状态向量(state vector) 而 t 代表时间。

计算机求解常微分方程

补充一下泰勒展开:
当函数 在点 处可导时，在点 的邻域内恒有:

一个很好的讲解(3bBlue1Brown)

如果我们从本质来看，可以更好的理解泰勒展开

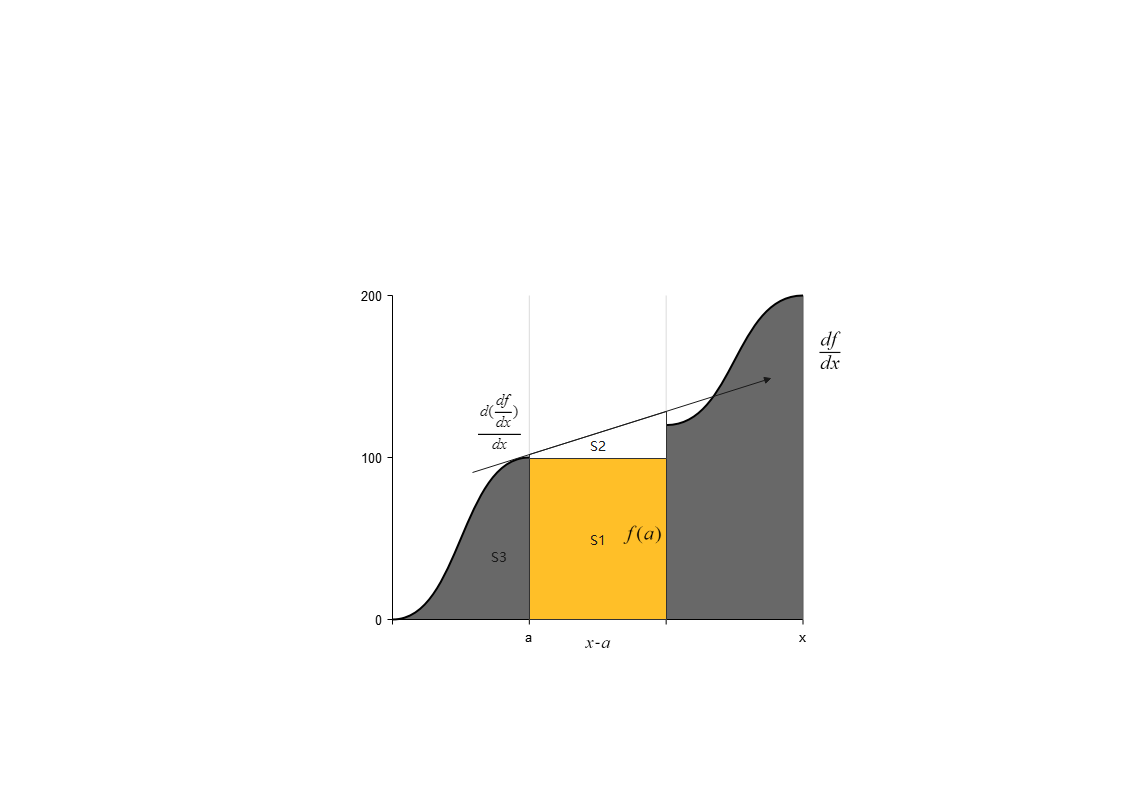
如上图，我们绘制了一个函数 的导数的图像，在这个 图像中, 的值可以用 和这个曲线围成的面积来计算。我们要求的 由三个部分组成：

• 
• 矩形
• 近似面积三角形

矩形的面积很简单，为长乘宽 , 我们取的三角形为图中 点导数与 构成的区域, 那么三角形的面积就是

这就是一个二阶的泰勒展开式，如果我们借助3阶甚至更高阶导数来进一步求面积，就会使结果更加的精确，就有了上面的泰勒展开式的形式。

显式欧拉法(Forward-Euler)

显示欧拉法的核心是用 来代替 , 这样在一阶泰勒展开式就可以用我们已知的量来计算未知的 的值。为了保证计算更加的精确，同时我们将从 到 分成若干个 , 我们通过步步迭代来求得最终的估计值。迭代的函数如下:

其中 为我们的估计值，而 就是当前累计迭代的 值，由于我们忽略掉了泰勒展开二阶以后的所有量，所以我们的这个方法只有一阶的精度。

隐式欧拉法(Backward-Euler)

和显示欧拉大部分相同，但有些微不同。不同就在于隐式欧拉法选择用 代替 , 这样如果对 在 处展开，就能得到一个包含未知数的方程的递推公式。

隐式欧拉也等价于找上述方程的解，如果这个解有解，那么自然近似值也有解，即隐式欧拉可以更加好的确保稳定性，这对于考察一些系统的长期行为有帮助（我们会在后面的代码中说明这一点）

龙格库塔法(Runge-Kutta)

龙格库塔方法是一种高阶的方法，注意这里的高阶并不意味着任何时候它更加精确，只是它在我们减小步长的时候更误差会降低的更小。实际上，以四阶龙格库塔法为例，当步长选的比较大的时候，它的误差甚至比显式欧拉法还大。（我们会在后面的代码中观察到这一现象）

下面介绍 RK4（4阶龙格库塔）方法，迭代公式如下:

以4阶龙格库塔方法为例，当我们减半，误差的值将会变为原来的 1/16，同样的低阶方法（如显示欧拉）只能将误差变为原来的 1/2。

代码

多数无益，我们用几个例子来比较一下这些方法

FE vs BE

# 显式欧拉和隐式欧拉的对比
import math
import matplotlib.pyplot as plt
import numpy as np

llam = 1
u0 = 3
t_final = 3 * math.pi
dt = 1e-1


def dudt(t, u):
    return -llam * (u - math.cos(t)) - math.sin(t)


def tf(t):
    return (u0 - 1) * math.exp(-llam * t) + math.cos(t)


def forward_euler(f, u0, dt, t_final):
    us = [u0]
    u = u0
    t = 0
    for i in range(0, int(t_final/dt)):
        u = u + dt * f(t, u)
        us.append(u)
        t += dt
    return us


def backward_euler(f, u0, dt, t_final, lam):

    # newton nonlinear solver function
    def newton(t, u, f, dt, lam):
        uu = u
        g = lambda x: ((x - u) / dt - f(t, x))
        j = lambda x: 1 / dt + lam
        for _ in range(1, 100):
            u_next = uu - g(uu) / j(uu)
            uu = u_next
            if abs(g(u_next)) <= 1e-14:
                break
        return uu

    us = [u0]
    u = u0
    t = 0
    for i in range(0, int(t_final/dt)):
        u = newton(t+dt, u, f, dt, lam)
        us.append(u)
        t += dt
    return us


t_true = np.linspace(0, t_final, 1000)
u_true = [tf(t) for t in t_true]
plt.plot(t_true, u_true, 'b', label="True Function")
t = [i*dt for i in range(0, int(t_final/dt)+1)]
uFE = forward_euler(dudt, u0, dt, t_final)
uBE = backward_euler(dudt, u0, dt, t_final, llam)
err_FE = np.mean([abs(uFE[i] - u_true[i]) for i in range(len(uFE))])
err_BE = np.mean([abs(uBE[i] - u_true[i]) for i in range(len(uFE))])
print("Error of Forward Euler: ", err_FE)
print("Error of Backward Euler: ", err_BE)
plt.plot(t, uFE, "r-", label="Forward Euler")
plt.plot(t, uBE, "g-", label="Backward Euler")
plt.legend()
plt.savefig("./fe_be.png")
plt.show()

我们前面提到了一般来说，隐式欧拉更加的精确并且稳定（但有例外，尤其是原函数是线性函数的时候，显式欧拉更加精确）。什么是稳定性呢，就是当函数变化的时候，我们的估值计算误差不会发生很大的浮动。

上面的代码对 cos 函数做了一个小小的修改，以便于稳定性的比较，当 llam 很小的时候（如代码中），我们看到如下图：

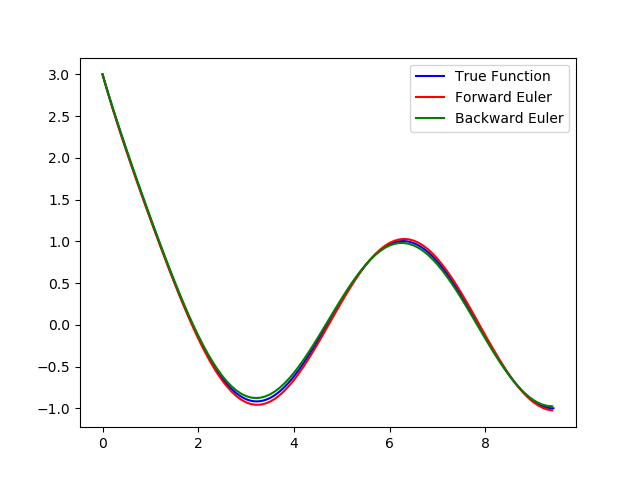
当我们将 llam 调到 100 的时候，就会发现图像变成了下面的样子：

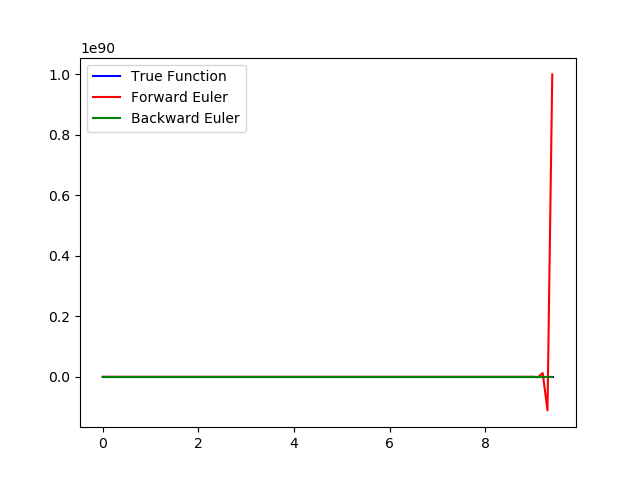
观察误差 Error of Forward Euler: 1.183439944385943e+88; Error of Backward Euler: 0.9107412532059388 明显，显式欧拉法的不稳定性弊端就凸显出来了。

计算隐式欧拉法的根的时候采用的牛顿法估计根，方法的描述如下图（懒得打了网上找了张图）

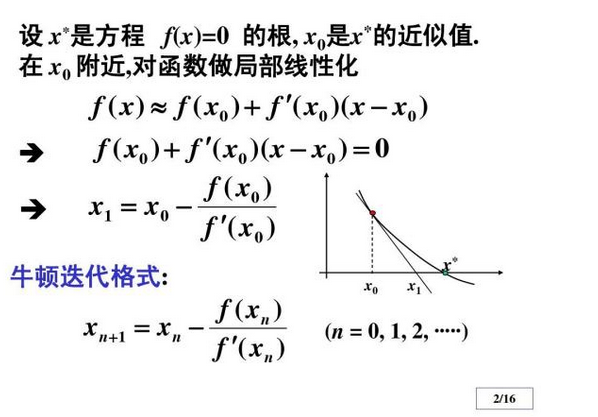
FE vs RK4

RK4 也并非一直都比 FE 更加的精确，看下面的这个例子：

我们设计下面一个 ODE：

令$ u(t)=e^{-\lambda t} \lambda$就可以比较 FE 和 RK4 方法的误差之处，有了真实函数方便我们计算误差，码来

import math
import matplotlib.pyplot as plt

coff = 100  # 1 10 100 尝试变化
u0 = 1
t_final = 1
fe_error = []
rk4_error = []


def f(t, u):
    return -coff * u


def true_f(u):
    return u0 * math.exp(-coff*u)


def forward_euler(f, u0, dt, t_final):
    t = 0
    u = u0
    while t < t_final:
        u = u + dt * f(t, u)
        t = t + dt
    return u


def rk4(f, u0, dt, t_final):
    t = 0
    u = u0
    while t < t_final:
        t_half = t + 0.5 * dt
        t_next = t + dt
        k1 = dt * f(t, u)
        u1 = u + 0.5 * k1
        k2 = dt * f(t_half, u1)
        u2 = u + 0.5 * k2
        k3 = dt * f(t_half, u2)
        u3 = u + k3
        k4 = dt * f(t_next, u3)
        u = u + (1/6) * (k1 + 2 * (k2 + k3) + k4)
        # 更新 t
        t = t_next
    return u


dt_vec = [1e-4, 2e-4, 1e-3, 2e-3, 1e-2, 2e-2, 1e-1]
for i in range(0, len(dt_vec)):
    dt = dt_vec[i]
    fe_result = forward_euler(f, u0, dt, t_final)
    rk_result = rk4(f, u0, dt, t_final)
    fe_error.append(abs(true_f(t_final) - fe_result))
    rk4_error.append(abs(true_f(t_final) - rk_result))

# 绘图
plt.loglog(dt_vec, fe_error, "r-", label="Forward Euler Error")
plt.loglog(dt_vec, rk4_error, "b", label="RK4 Error")
plt.xlabel("dt")
# y 轴设置反向
# ax = plt.gca()
# ax.invert_yaxis()

plt.ylabel("error")
plt.legend()
plt.savefig("fe_rk.png")
plt.show()

当我们取 时

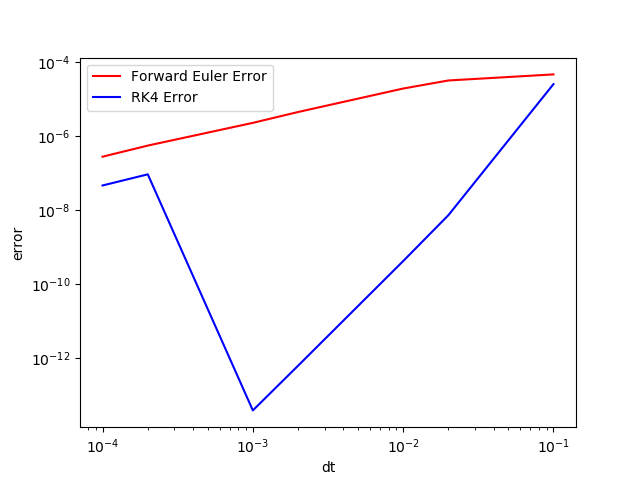
当我们取 时

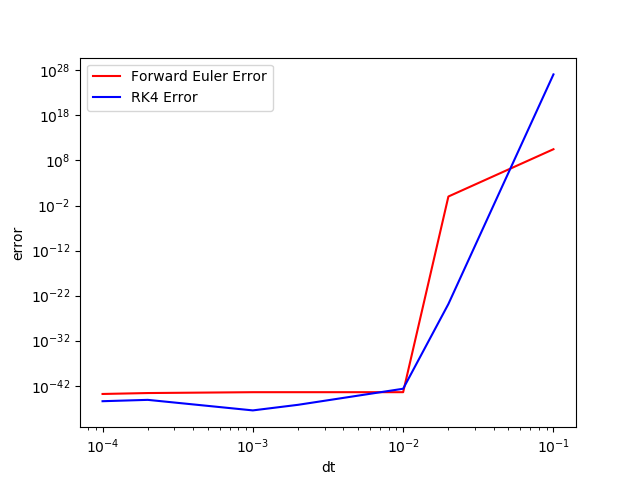
我们可以明显的感受到，并非高阶方法就能带来更小的误差，高阶只代表随着计算迭代次数增加，误差收敛的快。但这同时也要求有一个很好的 的选择。通常在对精度要求不高的计算中，我们都可以选择 FE 来解决。

(ps: 实际运算的时候 matlab 和 python 结果有些不同，matlab 更加精确一些，图像看起来也更好看。但图像变换的趋势和结论是一样的)