汇编基础
Posted Updated ComputerOrganization

汇编基础

整数运算

本章将学习汇编语言的最大优势之一:基本二进制位移和循环位移技术。实际上，位操作是计算机图形学，数据加密和硬件控制的固有部分。

位移动(bit shifting)

移动操作数的位有两种方法，
第一种: 逻辑位移(logic shift)，空出的位用0填充
第二种：算数位移(arithmetic shift)，空出的位用原数据的符号位填充

符号 说明
SHL 左移
SHR 右移
SAL 算数左移
SAR 算数右移
  • 位移操作的最高位或最低位都会被复制到CF(进位标志位)
  • 当一个数多次右移时，进位标志位保存的是最后移出最低有效位的数值
  • 最高有效位(MSB),最低有效位(LSB)

例子:

有符号除法

1
2
mov dl, -128   ;DL=10000000b
sar dl, 3      ;DL=11110000b

即用SAR实现有符号数除以2的整数次幂

AX符号扩展到EAX

1
2
3
mov ax, -128   ;EAX=????FF80h
shl eax, 16    ;EAX=FF800000h
sar eax, 16    ;EAX=FFFFFF80h

先左移16位然后算数右移16位就完成了将AX符号扩展到EAX

位元循环(Bitwise Rotation)

以循环的方式来移位，不会弃位，从数的一段循环出去的位会在该数的另一端出现

符号 说明
ROL 循环左移
ROR 循环右移
RCL 带进位的循环左移
RCR 带进位的循环右移
  • ROL和ROR同样最高位和最低位会被复制到CF中
  • RCL和RCR会将最高位或最低位移动到CF中，CF移动到最低位或最高位

例子:

循环多次

1
2
mov al, 00100000b
rol al,3           ;CF=1,AL=0000001b

位组交换

1
2
mov al, 26h
rol al, 4    ;AL=62h

利用ROL可以交换一个字节的高四位和低四位

从进位标志位恢复位

1
2
3
4
5
6
.data
val BYTE 01101010b
.code
shr val, 1  ;LSB(最低有效位)移入标志位
jc exit     ;为1退出
rcl val, 1  ;否则恢复

有符号数溢出

如果有符号数循环移动1位生成的结果超过了目的操作数的有符号数范围，就发生了溢出

1
2
mov al, +127
rol al, 1   ;OF=1,溢出al变为负数-2

如果循环次数大于1，则溢出标志位无定义

SHLD/SHRD

SHLD(双精度左移)指令将目的操作数向左移动指定位数，形成的空位由源操作数的高位填充，最高位移动到CF。同理SHRD。

Q:编写一组指令不使用SHRD将AX的最低位移入BX的最高位
A：

1
2
ror ax, 1
rcr bx, 1

K：即借用CF作为中转站，我们若想对数组进行移位操作，思路和该方法一样

Q：计算EAX中32位数奇偶性的方法之一是利用循环把该数的每一位都移动进入进位标志位，然后计算进位标志位置1的次数，根据结果设置奇偶标志位
A：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
.386
.model flat, stdcall
.stack 4096
ExitProcess PROTO,dwExitCode: DWORD

.code
main PROC
    mov eax, 1111b
	mov ecx, 32
	mov esi, 0
L1:
    rol eax, 1
	jnc L2
	inc esi
L2:
    loop L1

	shr esi, 1
	jc L4
	mov ebx, 11
	jmp L5
L4:
    mov ebx, 1
L5:
    xor ebx, 0
main ENDP
END main

其实后面的代码意义不大,目的在于置奇偶标志位，若esi为偶数，则最低位一定是0，反之为奇数

乘除指令

Q:请说明执行MUL指令和单操作数的IMUL指令时，不会发生溢出的原因
A:MUL指令（无符号数乘法）中的单操作数是乘数，如下表列出了默认的被乘数和乘积。由于目的操作数是被乘数和乘数大小的2倍，所以不会溢出

被乘数 乘数 乘积
AL reg/mem8 AX
AX reg/mem16 DX:AX
EAX reg/mem32 EDX:EAX

Q：生成乘积时，单操作数IMUL和MUL指令有何不同？
A：IMUL（有符号数乘法）执行有符号的整数乘法，与MUL不同的是IMUL会保留乘积的符号

Q：什么情况下单操作数IMUL会将进位标志位和溢出标志位置1？
A：与MUL指令一样，其乘积的存储大小使其不会发生溢出。同时，如果乘积的高半部分不是其低半部分的符号扩展，则进位标志位和溢出标志位置1

  • 单操作数下，将乘积存放在AX，DX：AX，EDX：EAX中
  • 双操作数下第一个操作数必须是寄存器，第二个可以是寄存器，内存操作数，立即数。会将结果放在第一个寄存器中
  • 三操作数下第一个是结果保存的寄存器，第二个是reg/mem，第三个是imm，表示将立即数和寄存器/内存数相乘放入第一个寄存器中

注意：二三个操作数时若寄存器大小不够，会按大小低位截取，并将溢出和进位置1

Q：DIV指令中，若EBX为操作数，商保存在哪个寄存器？BX为操作数呢？
A：

被除数 除数 商 余数
AX reg/mem8 AL AH
DX:AX reg/mem16 AX DX
EDX:EAX reg/mem32 EAX EDX

Q:有符号除法和无符号的区别是？
A：几乎完全相同，只有一个重要区别，在执行除法前，必须对被除数进行符号扩展（将一个数的最高位复制到包含该数的变量或寄存器的所有高位中）
K：3种符号扩展指令CWD（字转双字），CBW（字节转字），CDQ（双字转四字）

例子：

1
2
3
4
5
6
7
.data
wordVal SWORD -101
.code
mov dx, 0
mov ax, wordVal    ;DX:AX=0000009Bh(+155)
mov bx, 2
idiv bx

结果并不是我们想要的，因为我们的DX和AX组合时忽略了符号问题
加上cwd即可，此时DX：AX=FFFFFF9Bh

  • 关于CWD的更多说明(2019.11.14修改)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
CBW     AL -> AX
执行操作： 
若(AL)的最高有效位为0，则(AH)= 00H
若(AL)的最高有效位为1，则(AH)= FFH

CWD     AX -> (DX,AX)
执行操作：
若(AX)的最高有效位为0，则(DX)= 0000H
若(AX)的最高有效位为1，则(DX)= FFFFH
例子:
(AX) = 0BA45H
CBW      ; (AX)=0045H
CWD      ; (DX)=0FFFFH  (AX)=0BA45H

其主要作用之一就是将我们的数据进行符号扩展或截断，就想题目中一样，我们想要用dx:ax做除法的除数，但我们的数仅仅有16位，对dx清零后直接用dx和ax组合会有符号的问题，这时候进行一下符号的扩展就能解决符号的问题

扩展加减法

扩展精度加减法（extended precision addition and subtraction）是对基本没有大小限制的数进行加减法。比如在C++中，没有标准运算符会允许两个1024位整数相加，但在汇编中，ADC（带进位加法），SBB（带借位减法）就适合这样的操作。

例子：两组数的相加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
INCLUDE Irvine32.inc

.data
op1 BYTE 34h, 12h, 98h, 74h, 06h, 0A4h, 0B4h, 0A2h
op2 BYTE 02h, 45h, 23h, 00h, 00h, 87h, 10h, 80h
sum BYTE 9 DUP(0)

.code
main PROC
    mov esi, OFFSET op1
	mov edi, OFFSET op2
	mov ebx, OFFSET sum
	mov ecx, LENGTHOF op1
	call ExtendedAdd

	;显示和数
	mov esi, OFFSET sum
	mov ecx, LENGTHOF sum
	call DisplaySum
	call Crlf
	call WaitMsg
	exit
main ENDP

ExtendedAdd PROC
;------------------
;计算两个以字节数组存放的扩展整数的和
;参数：ESI和EDI存放两个加数数组的指针，EBX为和变量的指针，ECX为相加字节数
;无返回
;------------------
    pushad
	clc              ;清除标志位

L1:
    mov al, [esi]
	adc al, [edi]
	pushfd           ;保存进位标志位
	mov [ebx], al    ;保存部分和

	add esi, 1
	add edi, 1
	add ebx, 1
	popfd            ;恢复标志位
	loop L1

	mov BYTE PTR [ebx], 0   ;清除和数高字节
	adc BYTE PTR [ebx], 0   ;加上进位
	popad
	ret
ExtendedAdd ENDP

DisplaySum PROC
    pushad
	;指向最后一个数组元素
	add esi, ecx       
	sub esi, TYPE BYTE
	mov ebx, TYPE BYTE
L1:
    mov al, [esi]
	call WriteHexB      ;显示该字节
	sub esi, TYPE BYTE
	loop L1

	popad
	ret
DisplaySum ENDP
END main
  • 注意我们的核心过程ExtendedAdd，每次循环使用adc并压栈进位标志位，为的是后面的add不影响我们的进位，循环前恢复就可以在下次做adc运算是加上了
  • 最后一步是检查操作数的最高位是否产生了进位，有进位就放入sum的最高位

ASCII和非压缩10进制

BCD码

用二进制编码的十进制数，通过专门的十进制数运算指令进行处理。计算机中可有专门的逻辑线路支持BCD码运算

压缩BCD

用4位二进制数表示1位十进制数，如：( 59 )10 ＝( 0101 1001 )BCD

非压缩BCD

用8位二进制数表示1位十进制数，如：( 59 )10 ＝( 0000 0101 0000 1001 )BCD

数字的 ASCII 码是一种 非压缩的 BCD 码

十进制调整指令

对于两个十进制数求和：
1.我们可以都转成2进制然后求和再转回10进制

2.直接进行字符串加法，再进行调整

相较于第二种方法，第一种方法过于麻烦，我们不会使用
而第二种方法的误差是统一的：
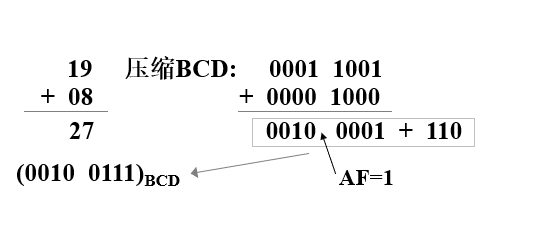
误差.png

所以可以设计指令来修正这个误差，当然也可以手动修正

非压缩的BCD码调整指令

命令 说明
AAA 执行加法后调整
AAS 执行减法后调整
AAM 执行乘法后调整
AAD 执行除法后调整

非压缩十进制数的最高位为0000b，而ASCII十进制数的最高位为0011b，任何情况下这两种类型的数字占一个字节
ASCII运算要比二进制运算慢的多，但在处理实数时不会出现浮点数运算的舍入误差的危险

1
2
3
4
5
mov ah, 0      ;记得清零
mov al, '8'    ;AX=0038h
add al, '2'    ;AX=006Ah
aaa            ;AX=0100h（01 00）
or ax, 3030h   ;AX=3130h='10'（31 30）

我们发现经过调整，2+8得到了10，而不是16进制相加的结果。而or ax, 3030h把10转变为了字符串’10’

压缩BCD码调整指令

仅用于32位模式

压缩十进制数的每个字节存放两个十进制数，每个数字用4位表示，如果数字个数为奇数，最高的半字节用0填充（有点像8421码的编码理念）
压缩十进制数的优势在于：

1.数据可以几乎包含含有任意数字的有效数字

2.与ASCII码的转换相对简单

DAA，DAS分别为调整压缩十进制数的加法和减法，我们会在练习题中使用它们解决问题

写在后面

果然返校后效率激增
充分证明在家里的学习环境没有学校好，或者是我太咕了
总共13章，加把劲在开学前看完

汇编基础

http://cyx0706.github.io/2019/08/03/AssemblyLanguageBasis-5/

Author

Ctwo

Posted on

2019-08-03

Updated on

2020-10-25

Licensed under

#

Comments

×